ながめも

競技プログラミングについて

RSUを売る方法

生活防衛資金補充のためRSUを売却したのでその備忘録。

1. 銀行を開設する

SBI新生銀行の口座を開設した。口座開設手続きはすべてオンラインで完結した。

SBI新生銀行を選択した理由は以下2点。

  • 外貨送金の手数料が無料なこと。

  • ドルから円への通貨変換手数料が割安なこと。

他に住信SBIネット銀行やソニー銀行なども選択肢に入る。

2. モルガン・スタンレー口座から売却する

モルガン・スタンレーの口座にログインして、売却手続きをする。

基本的には取得時価値が高いものから貪欲に選択すると当該年度の所得を抑えることができる（はず）。 株価が単調増加なら最新のものから売ればいいが、単調増加ではないため、自分で選んだ方がいい気がしている。 送付先には1. で開設した銀行口座を指定する。

モルガン・スタンレーから「売却できたよ」というメールが来るまで待つ。

3. 銀行で受け取りのために必要な手続きをする

モルガン・スタンレーからSBI新生銀行に送金通知がいくと、口座持ち主に海外送金のための理由を聞くためのメールが届くので回答する。

その前にマイナンバーの設定をしておかないといけなかったらしい。これは一度やれば済む話だと思われる。あと引っ越しも同時にやっていたので住所も変更した。いろいろ並行しており手続きが謎の状態でスタックしないか心配。

2026/3/14時点では以上。送金が完了したらより詳細を追記する。

確定申告2024 備忘録

2025年3月17日〆切の確定申告2024を2025年3月14日に完了しました。本ブログでは確定申告で何をしなければならないのか、来年の私に向けて備忘録を残します。

  • 源泉徴収票
    • 年末に会社から郵送される。
    • オンラインでも閲覧可能なので紙を無くしても問題なし。
  • RSU
    • 給与所得。源泉徴収票を2枚以上と指定する。
    • vestの日付とドル建ての株価、ドル円から日本円で収入を計算し記入。
    • 源泉徴収税額はRSUの受け取り方によるが、「現金で払う」を指定してる場合は0。
  • ふるさと納税
    • ふるなびでまとめた。xmlの申し込み済み。2日かかるらしい。なんでやねん。
    • 1日で完了した。なんでやねん。
  • 医療費控除
    • 申告者本人はマイナポータルで同期。
    • 申告者の配偶者は、申告者本人を代理人に設定後、マイナポータル連携可能。
    • 代理人設定は、数年で期限が切れるため再度設定必要。
    • 自費診療分は任意で申告可能。
    • 歯の保険外診療も追加で申告可能。
    • 公共交通機関の交通費も申告可能。歩行困難な場合はタクシーも可。
    • 治療に必要と判断される場合、ドラッグストアなどで購入した医薬品も申請可能。
  • 生命保険料控除
    • 年末調整 or/and 確定申告.
    • 年末調整で会社に提出しなかった場合、確定申告。
    • 年末調整も確定申告もマイナポータル連携可能。
    • マイナポータル連携なら原本提出必要なし。

2023年の振り返り

去年の振り返り記事はこちら。

coonevo.hatenablog.com

2023年も大晦日となりましたので、簡単に今年を振り返ります。

仕事

2023年は仕事としてはソフトウェアの私としては大きめな部分の責任を負ったり、初めて海外出張したり、障害対応が当社比でできるようになったり、小さめのプロジェクトのマネジメント（？）に挑戦したり、など、挑戦と挫折、成長それぞれできたと思える一年でした。

海外出張ではその意義を理解でき、来年も別の機会で連れていってもらえるように仕事を作ろうとポジティブな影響を受けることができました。

障害対応は苦手意識があったのですが、開発経験を積んだこと、メンバーに質問して仕様を理解することに努めたことで、得意とは言わないまでも苦手意識を持つことはなくなったかなと思っています。やっぱり作って壊しまくるのが大事だと思いました。

プロジェクトマネジメントは挑戦する機会をいただいたのにも関わらず、挫折しました。他人を上手に動かす方法、数年単位の先を見据えてタスクを処理する方法がわかりませんでした。わからなかったので外してもらうという、チームや上司には迷惑なこともしてしまい申し訳ない気持ちもありますが、マネジメントするほどの開発経験が足りてないと判断しソースコードと対峙する時間を持つという別の目的を持っていて、その通りに過ごせた結果別の面で成長することもできたので、結果的にはいい判断だったと思っています。来年はマネジメントに再度挑戦します。一度挫折したことで何が大切なのかを意識することもできたので、次は逃げ出さないようにしたいです。

生活

体調を崩す日々も多く、通院の機会が増えました。通院すると体に気を遣えるようになるので、いい傾向だとは思います。これからも健康に気を遣って生きていきたいです。

まとめ

2024年は技術的な成長と人間的な成長という2つの柱で走っていこうと思います。

仕事以外のところで技術的な学びが少なすぎるので、幅を広げるために読書を習慣化します。競技プログラミングは・・・AHCにもっと参加したいなあ。

2024年もよろしくお願いします。

2022年の振り返り

日記

まずは去年の目標を振り返ります。お酒飲んでるので変なこと書いてあっても許してください。

2022年の目標は、以下の記事にある通り coonevo.hatenablog.com

コンピュータサイエンス全般、競技プログラミング、英語、読書

とありました。

コンピュータサイエンス全般については、勉強する時間を取れなかったので、来年は意識します。積読すごいので...

競技プログラミングは、

というように、レートは上がっていたみたいです。

英語は、オンライン英会話の退会に成功（？）しました...。仕事で話す機会も増えてきた、これからも増える、ようなので、再開しようかな...。オンライン英会話をしていた効果は多少あって、臆せず話せるようにはなってる感覚はありますが、語彙力不足を雰囲気でカバーする、リスニングもダメダメ、みたいな感じだったので、先行きが不安です。

読書は、積読が増えるばかりでしたが、仕事術というか、仕事論みたいな部分ですごく感銘を受けた本が二冊、印象に残っています。

どちらの本も、私の所属する組織で自然と、当たり前のように行われていることが、なぜ行われるようになったのか、どういう意味があるのか、ということを明確に言語化されており、読んだことで仕事がしやすくなりました。おすすめです。

2022年は、社会人2年目であり、結婚したりと、変化に富んだ一年でした。

会社員としては、ありがたいことに、大きな仕事の小さくない部分を任せていただき、この業界で生きていく上で礎となるであろうことを学びました。失敗もありましたし、成功もありました。考えすぎてしまったこともありましたが、深く考え続けてよかったこともありました。何より、ユーザーの喜びが何にも変えがたいほど嬉しかったです。感謝の声が人づてに届いたときの気持ちは一生忘れない気がします。これからも、私の持っている技術で、誰かを喜ばせられるような仕事を探していきたいものです。

生活面としては、結婚しましたが、元から同棲していたので、ほぼ生活に変化はないです。郊外の広めの部屋に住んでいますが、自炊もしやすいですし、物価も安いですし、必要なときに人混みにいく程度が自分にはあってるような気もします。移動にかかる時間は無視できないくらい大きいので、たまにうーんとなりますが、大きめの洗濯機と冷蔵庫で家事の負担軽減をしてなんとか耐えています。いつまで耐えられるかな、という感じなので、そのうち引っ越すとは思います。東京の家賃高すぎるよ...

これは番外編になりますが、たまにキャリアに悩んでTwitterに真面目なことを書くと反応してくれる優しいフォロワーさんに、この場を借りて深く感謝申し上げます。仕事ばかりしてると気づかない新しい視点に立つことができています。いつもありがとうございます...

2023年の目標については年明け時間があるときにまた考えます。皆様よいお年を。

AHC011に参加しました

AHC マラソン

173位でした。

gitのコミットを見て時系列で振り返っていきます。

5/28（1日目）

問題文を読む。グリッドで操作も簡単な好みな問題だと感じ、力を入れて参加することを決意。

コミットを読むに、タイルクラスを追加したり、ジャッジを実装してた。 深夜まで実装してます、この人。

5/29（2日目）

ツイートにも履歴がないため何もしてないですね。昼まで寝てた気がします。移動が多かったかな？

5/30（3日目）

だそうです。

5/31（4日目）

かわいそう。でも腰が痛いのに取り組んでますね、えらい。

この日の夜は、最終状態を何かしらの方法で探したいと思っていました。 dfsで探そうとしたんですが、何を思ったのか、一本道を構成するdfsを書いていました。疲れていたんでしょうね。「dfs ダメ」と残したままmasterブランチを捨てています。

6/1（5日目）

通勤電車の中で考察してました。

前日に謎のDFSを書いていた私ですが、朝になって冷静になり、みんなのseed=0の共有画像を見比べながら、多様だしランダムにやっても意外と枝刈りのおかげで木ができるんじゃないか？と妄想してました。

夜になったので実装しようとします

6/2（6日目）

寝落ちしたそうです。大変そうですね。

仕事の後は空を眺めてました。

この日も疲れて何もできてなさそうです。

6/3（7日目）

この日も仕事です。

6/4（8日目）

土曜日なのでお休みです。お昼ごろから取り組みます。

ねてたそうです

頑張ってください

残り2日しかないので頑張って実装します。

木の構築

まずは2点swapの山登りで木を構築しました。 それなりに強めの枝刈りを入れると100 msくらいで見つかったりもするみたいです。運が悪いと1.5 secでも見つからなかったりしますが、諦めました。

行ごとに揃える

右の2列と下の2行以外を揃えるコードを書きました。動かしていいところがこれだけあると直感的な操作でマスを自在に動かせることを確認しました。

残ったところは山登りして、この時点で1.9M。結構いい。

6/5（9日目）

よく考えると最右端を残して揃えられるんじゃ？と思い実装したらできました。

列ごとに揃えていくと、最後2行は残ってしまうので、やっぱり手軽なランダム山登り。2.3Mに伸びました。

この後はREが起きたときにファイルに出力するようにしてデバッグを早くしてました。本当は最後の2行も解くための方法は思いついていたんですが、実装が重すぎて間に合わず。

皆さんの解法を見て、ビームサーチやchokudaiサーチも試してみたい気持ちになってます。

これが最終解答の動画です。

最後に

前回のマラソンの解説放送のときにwataさんが天才発想を披露していて、そんなの問題固有の話じゃ・・・とか思っていた私ですが、そのときの話を応用して今回楽しめたので、意外とこういうアドホックな部分が大事なんだろうなー思ったりしました。アドホックをアドホックとして終わらせないというか・・・

いかがでしたか？マラソンは楽しいので、みんなもやろう！

codingame:Spring Challenge 2022 ローカル対戦のための環境構築

Codingame、通称コドゲは、開発したゲームAIの強さを競うコンペを主催している会社のサイトです。先日Spring Challenge 2022が始まったばかりですね。

本記事では、Spring Challenge 2022でローカルで対戦する環境を構築するための方法について紹介します。 今回は最低限ローカルで動くところを目的としているため、便利なスクリプトを使った実行などについては触れません。最後に参考記事を載せておいたのでそちらを参考にしていただけたらと思います。また筆者の環境であるmacOS以外についても触れません。ご了承ください。

必要なもの

  • Java8
$ ls /Library/Java/JavaVirtualMachines/
jdk1.8.0_331.jdk

jdk-12.0.1.jdkなどでは動作確認してません。どれがいいのかわからないけど、とりあえず進めます。 Javaのinstall方法については他記事に任せてしまいますが、私はOracleの公式からダウンロードしました。

mavenって何？

Apache Maven is a software project management and comprehension tool. Based on the concept of a project object model (POM), Maven can manage a project's build, reporting and documentation from a central piece of information.

なるほど。インストールします。

$  brew install mvn

バージョンは、、

$ mvn --version
Apache Maven 3.8.5 (3599d3414f046de2324203b78ddcf9b5e4388aa0)
Maven home: /usr/local/Cellar/maven/3.8.5/libexec
Java version: 18, vendor: Homebrew, runtime: /usr/local/Cellar/openjdk/18/libexec/openjdk.jdk/Contents/Home
Default locale: en_JP, platform encoding: UTF-8
OS name: "mac os x", version: "10.15.7", arch: "x86_64", family: "mac"

最新です。これもどれがいいのかよくわからないけど動くのでよし！

学生さんは有料版（IntelliJ IDEA Ultimate） が無料で使えますが、 無料版（Community Edition）でも今回は特に問題ないです。

  • git

githubから公式が提供してる環境をダウンロードするのにあると便利です。

実行手順

  1. ローカルにプロジェクトをダウンロードする
  2. IntelliJでプロジェクトを読み込む
  3. 実行する

1. ローカルにプロジェクトをダウンロードする

こちらのrepositoryにあります。

github.com

任意の場所にcloneします。

$ git clone https://github.com/CodinGame/SpringChallenge2022.git
Cloning into 'SpringChallenge2022'...
remote: Enumerating objects: 124, done.
remote: Counting objects: 100% (124/124), done.
remote: Compressing objects: 100% (95/95), done.
remote: Total 124 (delta 20), reused 120 (delta 17), pack-reused 0
Receiving objects: 100% (124/124), 2.12 MiB | 6.79 MiB/s, done.
Resolving deltas: 100% (20/20), done.
$ ls
SpringChallenge2022

2. IntelliJでプロジェクトを読み込む

IntelliJを起動して右上のOpenからの先程のSpringChallenge2022フォルダを選択して開きます。

こんな画面になればOKです。

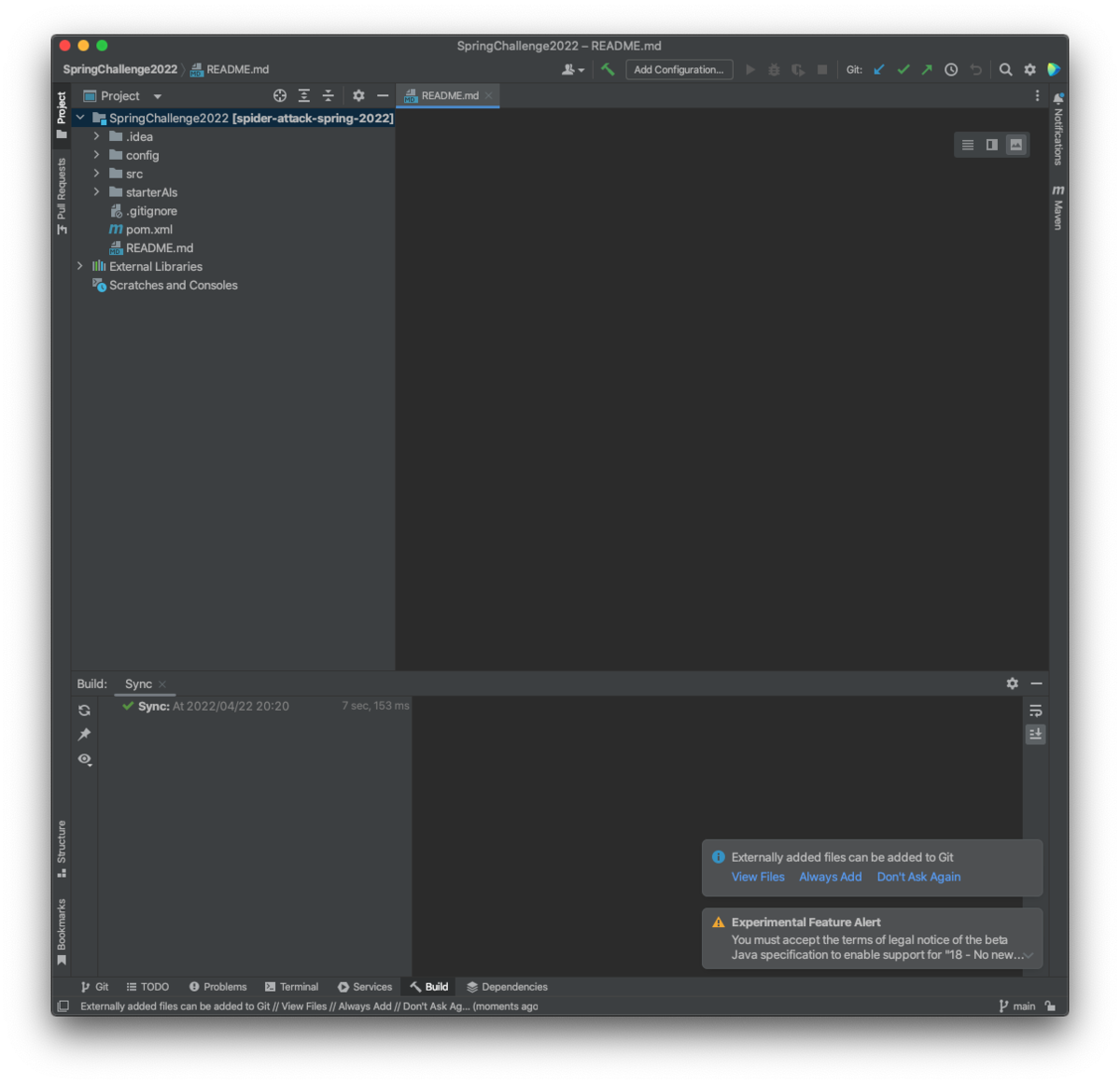
2.5 描画moduleにも手を加える

このまま3. に進むと実行はできるけど真っ暗となってしまいます。SpringChallenge2022では描画のリソースにも手を加える必要があるみたいです。npmを使います。

参考: github.com

$ npm --version
6.14.4
$ cd SpringChallenge2022/src/main/resources/view/ && npm ci && npm run start

[8:46:25 PM] File change detected. Starting incremental compilation...

[8:46:25 PM] Found 0 errors. Watching for file changes.

これでOKです。

3. IntelliJで実行する

実行のエントリポイントとなるファイルsrc/test/java/Main.javaを開きます。 compileJavaという関数を呼んでますが、ここのbashスクリプトの実行でこけると悲しいので、Player twoと同じくpythonのスターターに置き換えちゃいましょう。

これでpython vs pythonになりました。

public class Main {の行の左にある実行ボタン押してRun Main.main()を選択すると色々走って（依存関係の解決とかbuildとか？)実行されます。※

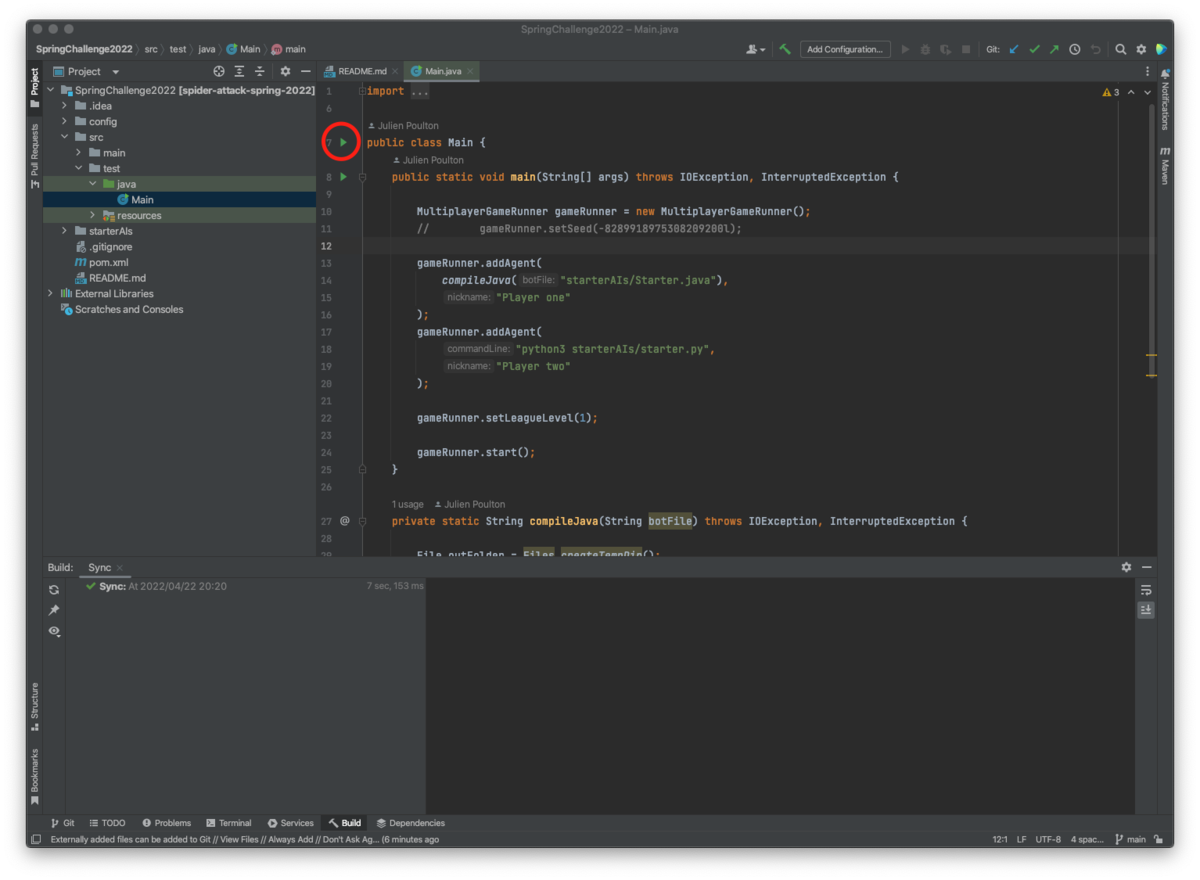
実行されました。http://localhost:8888/test.htmlにブラウザからアクセスしてみましょう！

うおー。

最後に

いかがでしたか？ローカル実行環境でAIを育てて、ライバルに差をつけよう！ 筆者はまだルールすら把握してません。対戦よろしくお願いします。

以下、過去の記事で参考にさせていただいたものです。わからないことなどあればこちらも参照ください。

koyumeishi.hatenablog.com

w.atwiki.jp

※ 環境によっては以下のようなエラーが出ます。Javaのバージョンが新しいもので実行されてしまってるということなので、設定を変えます。左下の設定ボタンからJava8で実行されるように変更し、Applyボタンを押してOKで閉じて実行しなおしてください。

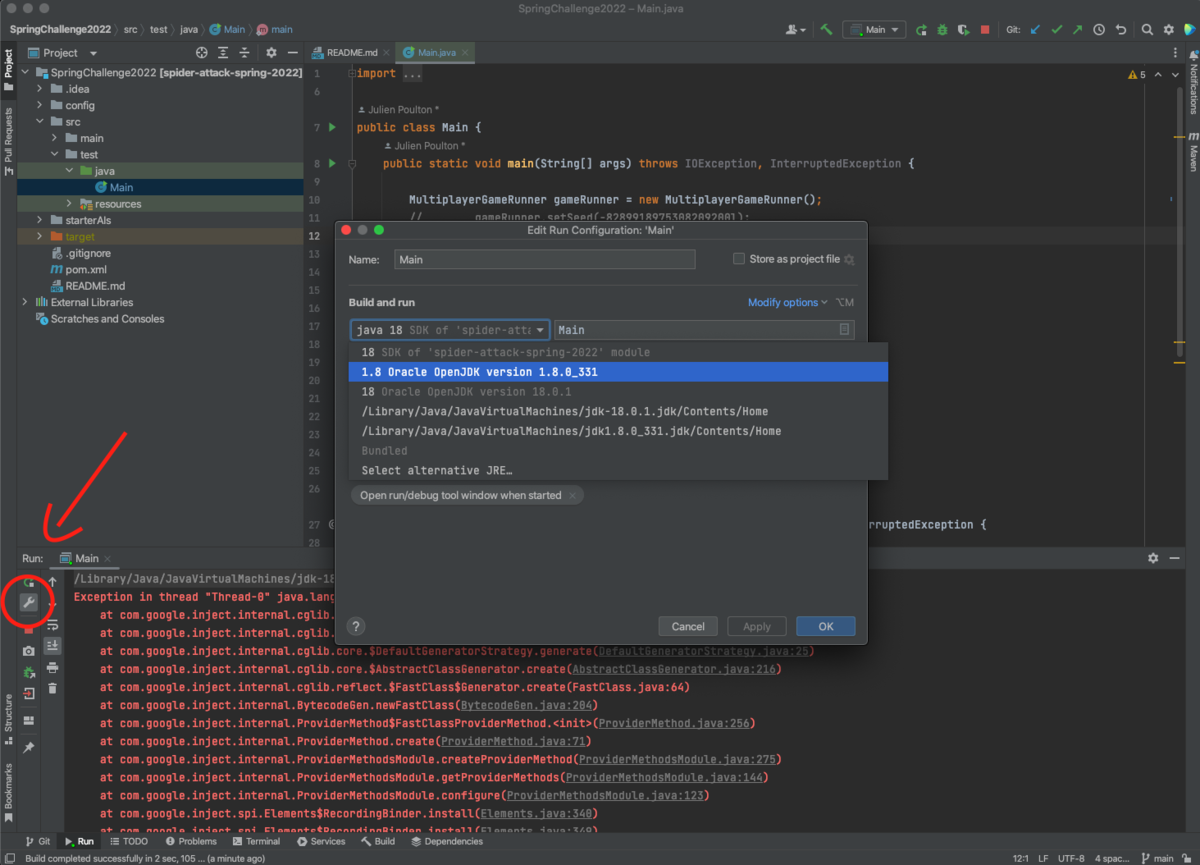
わからないことから一旦離れる勇気

わからないこと、知らないこと、できないことというのは、この世に無限にある。 知っていることの方が少ない。人間誰しもそういうものだ。

わからないことは恥ずかしいことではない。わかっていないことを、わかってふりをしていることが恥ずかしいのだ。

わからないことがあっても、前に進め。 わからないことを明確にする必要はない。ただ、わからないことを明確にしないなら、せめて、わかっていることを確実に知ろうとすることだ。

わからないことは、つまり、わかっていることではないことだ。 どこまでわかっているのかが明確になれば、わからないことをつぶす手がかりになる。

わからないこともわからないなら、とりあえず、進め。無視しろ。まだ早いのかもしれない。 いつか気づくから、その時まで待てばいい。

新卒で入社した私の場合、わからないことが多すぎた。でも、わからないからと、手を止める暇はなかった。

ある程度の理解で、とりあえず進んでみると、何かが見えてくる。 見えてきたタイミングで、理解を始めればいい。 その時でも遅くない。わからない人が、わかろうとしているなら、他人は待ってくれる。

一番やってはいけないのは、わからないことを、情報をとりにいけるのに、無視することだ。